 |
|
May 22, 2003
The past several weeks featured five, weekend-long educational events for the youthful organizers of Lyndon LaRouche’s Democratic Presidential campaign—in Los Angeles, Philadelphia, and three held simultaneously by telephone hook-up in Seattle, Germany, and Mexico. Each of these intensive educational weekends, which we have called cadre schools, began with a short address by LaRouche, followed by a lengthy question-and-answer session with him, probing the deepest issues of philosophy, science, history, and art.
Each cadre school also featured what was termed a “pedagogical festival,” where demonstrations of physical scientific principles that had been worked out by the youth themselves were presented. These demonstrations were an inflection point in a long process of intellectual development, which we have carried out for the growing numbers of full-time and part-time activists of the LaRouche Youth Movement.
This process had really begun in earnest, when a small group of us in Los Angeles took up Lyndon LaRouche’s challenge to master Carl Friedrich Gauss’s 1799 proof of the Fundamental Theorem of Algebra.1 LaRouche challenged us to “know truth”—to go beyond the ability to repeat taught knowledge (in the way we were instructed in school), to be able to know how we know. He chose the mastery of the 1799 proof of the Fundamental Theorem to initiate this process.
 |
Robert Lucero
Author Sky Shields demonstrates helicoidal minimal surface formed by soap film. |
In that 1799 proof, Gauss demonstrates that, contrary to the lies of Euler, Lagrange, and the Bush Administration chickenhawks—neither mathematics, nor the universe, can be reduced to a set of a priori axioms and postulates, from which history supposedly unfolds inevitably, apart from mystical interventions by little green men, or the violent fits of arbitrary impositions of will by the Nietzschean mathematicians, and the would-be imperialists who have created them.
Our initial intent was to try to establish, in a small core group, a certain level of competence in, at least, reading the topics contained therein. The plan was then to disseminate this throughout the youth movement as a whole, in order to achieve the mental, moral, and strategic effects Lyndon LaRouche had called for. This all exploded much sooner than we had intended, however, when the rest of the youth movement, hearing that work on the Gauss paper had begun, insisted on broadening the work group.
It became clear that the problem of working through the Fundamental Theorem was not just a problem of the Fundamental Theorem. There existed an entire historical and intellectual context, “a geometry,” in which it first had to be situated. The bulk of what we needed in order to situate Gauss’s breakthrough properly, in terms of the historical fight as well as in terms of the epistemology, was contained in the pedagogical series “Riemann for Anti-Dummies,” assembled by one of our senior advisors, Bruce Director.2
In this series, Director and others, as part of a program leading up to mastering the mathematics of BernEard Riemann—which was required to understand the LaRouche-Riemann Method of economic forecasting—have presented a thorough working-through of elements of the work of Riemann’s teacher, Carl Friedrich Gauss. For the rest, we’ve begun a process that shouldn’t find a reason to slow down any time in the next 10 years or more.
What, Really, Is Algebra?
For instance: What is the system, algebra, that the algebraists LaGrange and Euler mystified? Is it really the deductive set of symbol manipulations learned, like seal training, in algebra class? As an antidote to such training, we acquired copies of the original algebra book, the Hisab al’Jabr w’al Maqabala, by Al Kwarizmi,3 to work out what this system, al’Jabr, really was, because we understood that it was this physical system that Gauss drove to the point of breakdown, in order to force a breakthrough into what he called a “higher space.” One group of students began a project of working, chapter by chapter, through Gauss’s Disquisitiones Arithmeticae,4 which Gauss worked on concurrently with his Fundamental Theorem paper (both of which were written in his late teens and early twenties). We created an environment where people are often up until two to four o’clock in the morning, working intensely on pedagogical projects, in small groups, mostly informally. This comes on top of the regular, scheduled, class sessions each week.
Pushing this process quickly brought out two, important problems: (1) We had far too many people for only one or two people to teach, and (2) people had severe blocks on the subject of mathematics.
The first of these was, of course, a welcome problem. It’s a characteristic problem of a healthy economic process. It was resolved by the development of a capability, later identified by another of our advisors, Jonathan Tennenbaum, as a “brigade system” (referring to the education of the French military engineering corps in the Ecole Polytechnique under Gaspard Monge and Lazare Carnot in the late 18th Century). We established a network, initially internal to the West Coast offices (Seattle, San Leandro, and Los Angeles), and which has now spread both nationally and internationally, for collaboration on pedagogical method, as opposed to simply the pedagogical topics.
This question of teaching, or pedagogical composition, effectively cemented the topic of discussion as being a subsuming idea, rather than simply the series of predicated facts which could be organized, like notes in a musical piece, to convey that idea. The effect was necessarily to force the adoption of a producer, as opposed to a consumer, identity for certain youth organizers. A consumer, such as an average American today, interacts with the world merely in terms of simple object relations. The consumer’s world is a series of objects—either of desire or of discomfort—and symbols, such as those of algebra (as presented in any modern textbook) severed from the physical universe, to be manipulated according to a set of rules, in order to obtain desired results.
The producer is capable of seeing an entire developmental process enfolded in every product, where the consumer only sees “things to buy.” Whether it is the economic history and human effort which bring a product into being, or the history of the human effort behind the idea from which a mathematics is derived: these should be the real objects of human thought. To the extent that this sense has been imparted throughout the movement, we have developed a far more efficient network of teachers than we would have otherwise.
Reinforcing this understanding is not easy. Most people have undergone so much Social Darwinist brainwashing in the course of their education, that they block themselves psychologically on certain subjects. Math is possibly the most common block, but this is true for all so-called “subjects”: “I’m not a math person”; “I’m not a history person”; “I’m not artistically inclined”; or, ‘I’m not into politics,” are all considered perfectly normal things to say, by current social standards. But, they are all absolutely absurd.
All human beings, all children, have a natural curiosity in all things. Only some sort of trauma in their youth would serve to sour them on different subjects. Math class is often this traumatic experience. Most math classes in elementary and high schools have the same Darwinist character as a dog breeder’s kennel. Instead of actually rediscovering the greatest ideas in human history, and making that process the subject of human mentation, students are trained to perform tricks (admittedly, sometimes spectacular feats of rote calculation) for which they are given treats and good grades. Some make it as prize show dogs, and are then tracked as math studs, to be mated under the watchful eye of a professor or peer review board. Others don’t quite make the cut, and are told to study liberal arts (or perhaps home economics).
In the end, nobody ends up knowing mathematics, but a few can perform great calculating feats on command. The rest end up with a different kind of traumatic damage—though both abuses need to be repaired, in order to sustain a functional revolutionary cadre. In this way, our Gauss and other pedagogical work served a dual function, as sort of psychoanalysis for the membership. Solving this second problem, served to aggravate the first, as youth movement members who had been terrified of the science work, say, six months before, finally decided to dive in, and needed to be caught up to the rest.
It was this apparatus that was brought to bear around the Los Angeles Cadre School, and pushed into a phase shift. Jonathan Tennenbaum presented the LaRouche Youth Movement with what he called a “shopping list” of pedagogical demonstrations. Among the included projects were:
- constructions for demonstrating Kepler’s determination of the planetary orbits;
- demonstrations of Fresnel’s work on light;
- Abraham Kaestner’s pioneering work on mathematics, which brought us Gauss, and later Riemann;
- a demonstration and constructions of Leonardo da Vinci and Luca Pacioli’s work on the Platonic solids and the golden section;
- a lead-in to Gauss’s work on the divisions of the circle;
- apparatuses to demonstrate da Vinci’s work on waves, founding the study of hydrodynamics, which led to Riemann’s anticipation of shockwaves in air;
- a presentation of the constructive principles behind Brunelleschi’s dome in Florence, including least surfaces, and the catenary; and finally,
- a physical demonstration of the Pythagorean comma, and the goldmine of paradoxes within music and the human voice.
This had the equivalent effect of a science-driver economic project5 for the members of the youth movement, forcing the development of new skills, in particular increasing the capability and experience at physical constructions and demonstrations of principle, including design and execution of the apparatuses involved, a capability which had been limited prior to this.
The idea now is to push this process even further. An intensive cross-continental project, studying the works of Lazare Carnot, Gaspard Monge, and the Ecole Polytechnique has begun. Also, projects have been either proposed or taken up on the geometry and engineering of Gaspard Monge, projective geometry, techniques for identifying a given surface by its local characteristics, Christiaan Huygen’s work on light and wave fronts, Leonardo da Vinci’s work on perspective and his work on translation of motion, and consistently coming back to mainstays such as Gottfried Leibniz’s differential calculus, and the other projects mentioned.
Multiple translation projects, from French and German original texts, into both English and Spanish, are also in the works. It is for this reason that LaRouche has dubbed us, no longer the “No-Future generation,” but rather a “Renaissance generation.” Much fun will be had, and much trouble caused, in the days, weeks, and months to come!
Notes
1. Carl Friedrich Gauss, “New Proof of the Theorem That Every Algebraic Rational Integral Function in One Variable Can Be Resolved into Real Factors of the First or the Second Degree” (Helmstedt: C.G. Feckeisen’s, 1799). English translation by Ernest Fanlreyer, Department of Mathematics, Fitchburg State College, available through http://www.theacademy2004.com
2. This entire series can be found on the website of the LaRouche Youth Movement, http://www.the
academy2004.com, in the “Riemann for Anti-Dummies” section.
3. Robert of Chester’s Latin Translation of the Algebra of Al-Khowarizmi with an Introduction, Critical Notes, and an English version by Louis Charles Karpinski (New York: The Macmillan Company, 1915).
4. Carl Friedrich Gauss, Eisquisquisitiones Arithmeticae, transl. Arthur A. Clarke, S.J. (New Haven: Yale University Press, 1966)
5. For more information on science-driver economic projects, like the Apollo Mission to the Moon, the Manhattan Project, the original Strategic Defense Initiative as proposed by Lyndon H. LaRouche, Jr., and the principle behind them, see Lyndon LaRouche’s essays “The Gravity of Economic Intentions: The Science Driver Principle in Economics,” and “SDI Revisited: In Defense of Strategy” at www.larouchepub.com.
|
|
|
Pythagoras Has One Professor
Freaking Out at Exodus to LaRouche
by Sky Shields
LaRouche Youth Movement organizers have been regularly deploying to college campuses throughout the United States and globally, attempting to provoke a discussion of the sort of ideas required to head off a civilizational crisis of war and depression. We generally succeed, but there have been a few notable exceptions.
Since we have emphasized mastery of the Pythgagorean Theorem (that is, understanding why it is true, not simply what the formula is) in our own educational work, organizers frequently challenge students they meet to produce a proof. The purpose is to demonstrate the difference between mere taught knowledge and actual understanding.
A reporter for the San Francisco State campus newspaper, the Golden Gater, was apparently provoked by such a challenge. We would have preferred that he try to think through the matter for himself. Instead, it appears he took the opposite approach, and sought the opinion of an “authority,” in this case the chairman of the college math department. This “expert’s” cited comments seemed so foolish to us, that we had a look at the curriculum he teaches. It proved to be a perfect example of the problem we are criticizing.
First, we cite the campus newspaper report:
“ ‘The idea of the missing fraction that represents the hole between one and two is more than 2500 years old, dating back to Pythagoras,’ says SF State Mathematics Department Chair Dr. David Meredith, who says he once lost a student to LaRouche’s ‘cult.’ He adds that modern mathematics instruction encourages students to learn and seek out new truths on their own, rather than mimicking math as taught.”
This author obtained the San Francisco State mathematics curriculum from the school’s website, to find out what is taught there, that Meredith claims allows students to “seek out new truths on their own.” This is from the book Elementary and Intermediate Algebra, available in the San Francisco State campus bookstore:
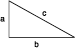
“A triangle is a right triangle if it has a 90° or right angle. The side opposite the 90° angle is called a hypotenuse. The other sides are called legs. In any right triangle, if a and b are the lengths of the legs and c is the hypotenuse, then a2 + b2 = c2” (Figure 1).
|
 |
|
Figure 1 |
|
|
That’s what the book’s authors call “the Pythagorean Theorem.” Now, what exactly does that formulation mean? Testing it on triangles, by substituting numbers for the lengths, a student would come to see that it seemed to “work” in every case—but why? Because the book says so?
The Pythagorean Theorem—or what’s left of it as taught here—has, like other algebraic techniques, such as FOIL (first, outer, inner, last), “completing the square,” the quadratic formula, and so on, the same significance to most modern math professors, and the victims of their malicious dog-show training, as a doll with stickpins does to a voodoo priestess: It is a mystical talisman, to be wielded in the same desperate way demonstrated by Euler, LaGrange, and D’Alembert, in Gauss’s account of their attempts to prove, using taught symbol manipulation, the Fundamental Theorem of Algebra. The actual algebra (al jabr) of Al Quarizmi (or Khowarizmi), which this textbook formulation obfuscates (as it also does the mathematical and philosophical work of Pythagoras and the Pythagoreans), takes a quite different, even antithetical, form.
The Real Theorem of Pythagoras
First, what does it mean to “square” a number? Is this simply the act of multiplying a given number by itself? If so, what does this have to do with the lengths of the sides of a right triangle?
The answer to this can be found in a general investigation of the properties of squares. Readers who are familiar with Plato’s Meno dialogue, or who have attempted to solve the problem of doubling the square, know that this cannot be accomplished by simply doubling the length of one side. This action gives a square four times as large as the original; tripling the side gives a square nine times as large, and so on (Figure 2).
|
 |
|
Figure 2 |
|
|
One can investigate the relationship between a length of line and the square constructed on it. It is a shorthand for this physical geometric relationship, which is later referred to as “squaring” a number. (Archytas, and later Gauss, demonstrate that this is a special case of a more general physical geometric conception of powers.)
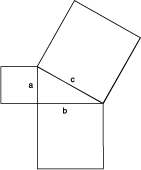
Now, looking back at our triangle, “a squared” would seem to mean the square built on length a. Our theorem would then look something like the image in Figure 3. But now, we have a new problem—how do you add one square to another, and still have a square? The reader should try different methods for this, before looking at the solution we will provide here.
|
 |
|
Figure 3 |
|
|
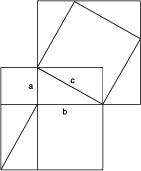
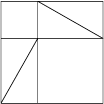
Now, for a demonstration (this is only one of many possible). Looking at our drawing, we see that several more triangles, each the same as our original, can be seen implicit in it. Draw these all in (Figure 4). Close inspection will reveal two identical squares in the construction, each with a side of combined length a + b, and each containing four of the original triangles as part of its area. (One of these identical squares is pictured, by itself, in Figure 5.)
|
 |
|
Figure 4 |
|
|
 |
|
Figure 5 |
|
|
Removing the same area from each of the two identical squares—in this case the four triangles—should give us the same remaining area. But, in the one case we have two squares, the a square and the b square, left over. In the other case, we have only one, the c square, left over. But, because of our construction, these areas must be equal! That is, a squared plus b squared must equal c squared.
“But, you can’t expect people to work through everything like this! It would take much too long!” might be the typical argument from one of today’s “new math” professors, or perhaps from a social climbing, young, aspiring political party hack (“This won’t help me get a high paying job! I just want to make friends and influence people.”)
But the truth is, that it is precisely because of the fact that most of those people whom we consider our political and intellectual leadership in the world today, have not worked through problems like this, that we are in the crisis we are in today. We have reached the end of a system, where all the currently accepted rules of economics, social relations, science, and mathematics no longer apply. And only if there is a movement in the world today, centered around rediscovering the method by which discoveries are made (not just consuming their by-products), will we be able to seek out the new ideas that are required to get us out of this mess.
|
|